【画像処理】2次元フーリエ変換と周波数フィルタリング
今回は周波数フィルタリングについて学んでいきます。
※空間フィルタリングについてはこちらの記事で説明しています。
2次元フーリエ変換とは？
フーリエ変換の基本概念
フーリエ変換は、時間領域（空間領域）の信号を周波数領域へ変換する数学的手法です。これにより、信号の周波数成分を解析し、特徴を抽出することができます。フーリエ変換の基本式は次のように表されます。
$$F(u) = \int_{-\infty}^{\infty} f(x) e^{-j2\pi ux} dx$$
この式は、関数 f(x) を複素指数関数で積分することで、各周波数成分の寄与を求めるものです。
2次元フーリエ変換
フーリエ変換は、画像を空間領域（spatial domain）から周波数領域（frequency domain）へ変換する数学的手法です。
画像処理では、2次元フーリエ変換（2D-FT）が用いられます。1次元フーリエ変換を x, y 方向に適用することで、画像の周波数成分を取得します。 $$F(u, v) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) e^{-j2\pi (ux + vy)} dx dy$$
ここで、jは虚数単位（ \(j = \sqrt{-1}\)）を表し、u, v はそれぞれ x 方向および y方向の空間周波数を示します。
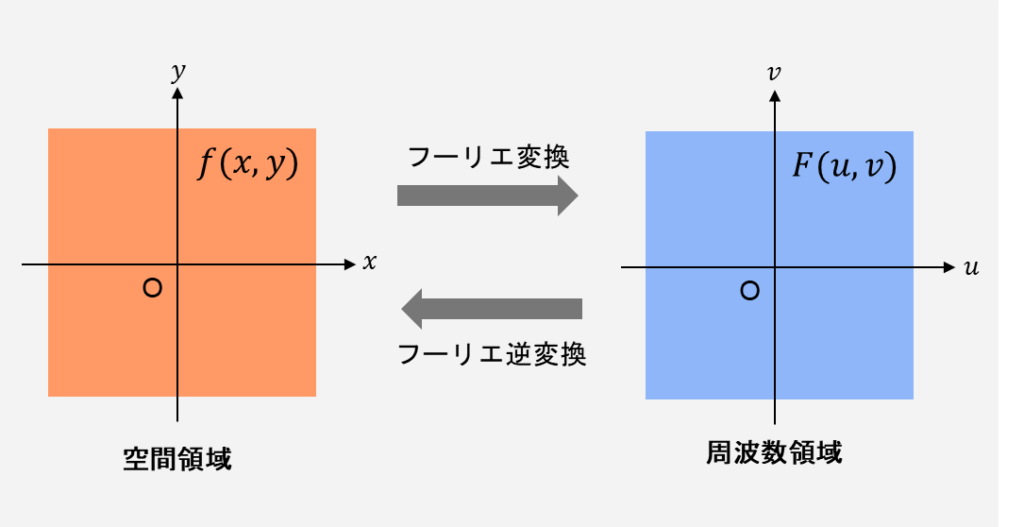
フーリエ変換を適用すると、空間座標 \((x, y)\)で表現される関数 \(f(x, y)\) により定義された画像が、周波数座標 \((u, v)\) で表現される関数 \(F(u, v)\)へと変換されます。
また、\(F(u,v)\)は以下に示すフーリエ逆変換により、元の画像\(f(x,y)\)に戻されます。
$$f(x, y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} F(u, v) e^{j2\pi (ux + vy)} du dv$$
フーリエ変換の特性
一般に、\(F(u,v)\)は複素数となるため、その特性を理解するために振幅スペクトルと位相スペクトルを考えます。
- 振幅スペクトル（Amplitude Spectrum）: \(|F(u,v)|\)
- 位相スペクトル（Phase Spectrum）: \(arg{F(u,v)}\)
- パワースペクトル（Power Spectrum）: \(|F(u,v)|^2\)
ディジタル画像に適用する際には、離散フーリエ変換（Discrete Fourier Transform: DFT）およびその逆変換（Inverse Discrete Fourier Transform: IDFT）が用いられます。
また、計算の高速化のために、高速フーリエ変換（Fast Fourier Transform: FFT）が実用的に広く使用されます。
フーリエ変換による画像解析
実際の画像に対するフーリエ変換結果を見てみます。
- Aの画像は高周波成分が少ないため、振幅スペクトルが中央に集中しています
- Bの画像は高周波成分を多く含むため、振幅スペクトルが周辺に広がっています
- Cの画像は、画像内にエッジが存在するため、エッジと直交する方向にスペクトルが広がっています
画像をフーリエ変換するとどうなるか
このように画像をフーリエ変換すると、周波数領域の表現が得られます。
画像のエネルギーは、低周波成分が中心に、高周波成分が外側に分布します。
周波数領域での画像の特徴
- 低周波成分: 画像の全体的な構造や滑らかな部分を表す。
- 高周波成分: エッジや細かいテクスチャを表す。
高周波・低周波成分の説明
- 低周波成分が多い画像はぼやけて見える。
- 高周波成分が多い画像はシャープだがノイズが多くなる。