コンピュータビジョンの基礎_カメラパラメータと座標変換
カメラパラメータの基本
カメラを用いた画像処理や3D再構成では、カメラの内部パラメータと外部パラメータを理解することが重要です。
カメラパラメータを使うことで座標変換を行うことができます。
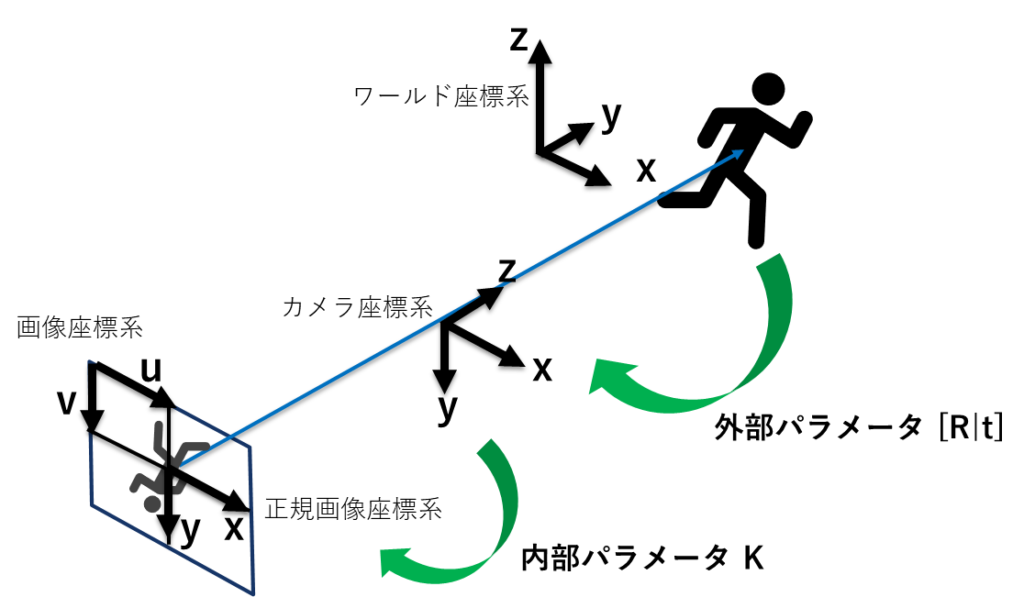
内部パラメータ(Intrinsic Parameters)
内部パラメータはカメラ固有の特性を表し、以下の要素を含みます。
- ワールド単位の焦点距離 (F): 実際のカメラレンズの焦点距離(物理単位)
- ワールド単位のピクセルサイズ (p_x, p_y): センサー上のピクセルの物理サイズ
- ピクセル単位の焦点距離 (f_x, f_y):センサーサイズとピクセルサイズに基づき、カメラの焦点距離をピクセル単位で表したもの。
$$f_x = \frac{F}{p_x}, \quad f_y = \frac{F}{p_y} $$ - 主点座標 (c_x, c_y): 画像中心のオフセット
- 歪み係数 (k_1, k_2, p_1, p_2, k_3): レンズの歪み補正に使用
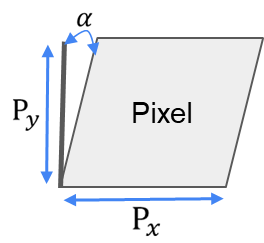
- せん断係数 (s): ピクセルの非直交性を補正するための係数
ピクセルのせん断は次のように定義されます。 \(s={f_x}{tan_α}\)
カメラ行列 (K):
$$K = \begin{bmatrix} f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}$$
ここで、せん断係数 sは、通常のカメラでは 0 ですが、非直交なピクセル形状を持つカメラでは補正が必要になります。
外部パラメータ(Extrinsic Parameters)
外部パラメータはカメラの位置と向きを表します。
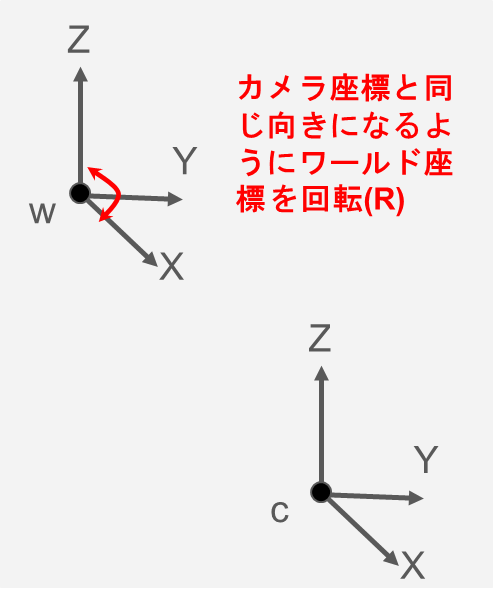
回転行列
回転行列 (R): ワールド座標系からカメラ座標系への回転
$$R= \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix}$$
回転行列は直交行列であり、カメラの向きを決定します。
※以下では回転行列 \(R\) の定義を詳しく解説しますので、不要な方はスキップしてください。
回転行列 \(R\) は、x, y, z 軸それぞれの回転行列\(R_x, R_y, R_z\) を掛け合わせることで求められます。回転の順序によって異なる結果になるため、適切な順序を選ぶことが重要です。
- x軸周りの回転: $$R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}$$
- y軸周りの回転: $$R_y(\theta) = \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix}$$
- z軸周りの回転: $$R_z(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$$
まず \(R_z\)、次に \(R_y\)、最後に \(R_x\) の順に回転を適用すると、最終的な回転行列 \(R\) は以下のようになります。$$R = R_x(\theta_x) R_y(\theta_y) R_z(\theta_z)$$具体的に展開すると、$$R = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta_x & -\sin\theta_x \\ 0 & \sin\theta_x & \cos\theta_x \end{bmatrix} \begin{bmatrix} \cos\theta_y & 0 & \sin\theta_y \\ 0 & 1 & 0 \\ -\sin\theta_y & 0 & \cos\theta_y \end{bmatrix} \begin{bmatrix} \cos\theta_z & -\sin\theta_z & 0 \\ \sin\theta_z & \cos\theta_z & 0 \\ 0 & 0 & 1 \end{bmatrix}$$
これを計算すると、$$R = \begin{bmatrix} \cos\theta_y \cos\theta_z & -\cos\theta_y \sin\theta_z & \sin\theta_y \\ \cos\theta_x \sin\theta_z + \sin\theta_x \sin\theta_y \cos\theta_z & \cos\theta_x \cos\theta_z – \sin\theta_x \sin\theta_y \sin\theta_z & -\sin\theta_x \cos\theta_y \\ \sin\theta_x \sin\theta_z – \cos\theta_x \sin\theta_y \cos\theta_z & \sin\theta_x \cos\theta_z + \cos\theta_x \sin\theta_y \sin\theta_z & \cos\theta_x \cos\theta_y \end{bmatrix}$$
$$ = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix}$$
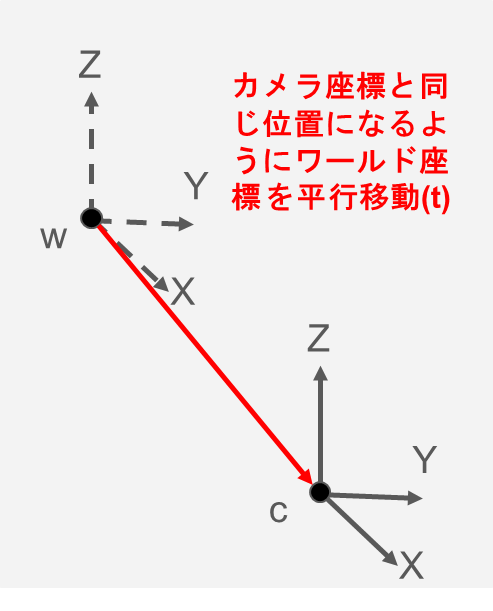
並進ベクトル
並進ベクトル (T): ワールド座標系からカメラ座標系への並進(平行移動) $$T = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}$$ 並進ベクトルはカメラの位置を示し、ワールド座標系からのオフセットを表します。
変換行列
変換行列 ( [R|T] ):この行列を用いて、ワールド座標からカメラ座標への変換を行うことができます。 $$P_{camera} = R \cdot P_{world} + T $$
$$\begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix}= R \cdot \begin{bmatrix} X_w \\ Y_w \\ Z_w \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}$$
ここで、 \(P_{world} = (X_w, Y_w, Z_w) \)はワールド座標系の点、\(P_{camera} = (X_c, Y_c, Z_c)\)はカメラ座標系の点を表します。
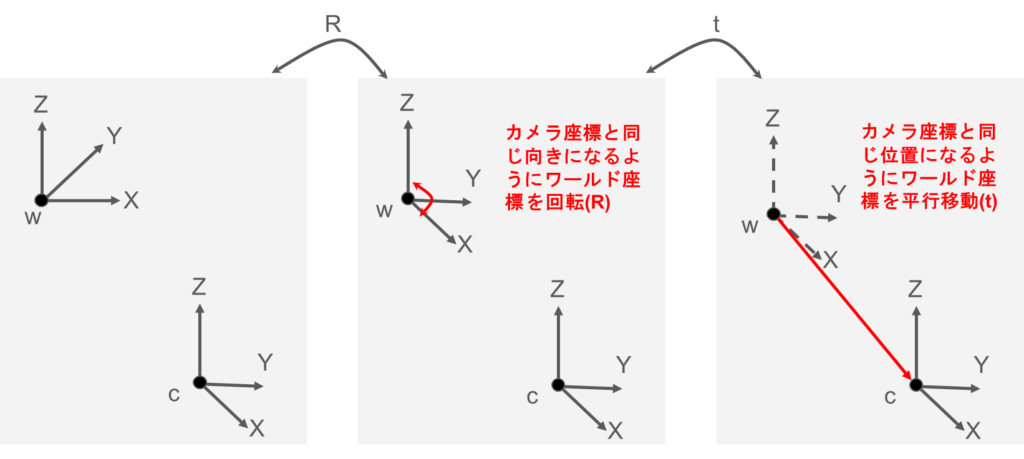
座標系の種類と変換
座標系の種類
- ワールド座標系: 3D空間上の基準となる座標系
- カメラ座標系: カメラ視点の3D座標系
- 画像座標系: 2D画像上のピクセル座標
こちらの記事で座標系について詳しく説明しています。
座標変換の流れ
- ワールド → カメラ座標系変換:
$$P_{camera} = R \cdot P_{world} + T$$ - カメラ → 画像座標系変換:
$$P_{image} = K \cdot P_{camera}$$ - 正規化(ホモグラフィ変換):
$$\begin{bmatrix} x’ \\ y’ \\ w’ \end{bmatrix} = K \cdot \begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix} $$
$$(x, y) = \left( \frac{x’}{w’}, \frac{y’}{w’} \right)$$











ディスカッション
コメント一覧
まだ、コメントがありません