【画像処理】空間フィルタリング_ラプラシアン/LoG/DoGフィルタ
画像の2次微分
前回の記事では基本的に画像の1次微分に相当する処理を説明しました。
ここでは、画像の2次微分に対応する処理について説明します。
2次微分は、微分を2回繰り返すことであり、ディジタル画像では差分を2回繰り返すことで求められます。
1次微分フィルタは、それぞれ注目画素の右と左に半画素ずれた位置の差分値を求めていると解釈できます。そのため、それぞれのフィルタの出力の差を求めれば、ちょうど注目画素位置の2次微分を求めることになります。
ラプラシアンフィルタ
さらに、2次微分の値を用いてラプラシアンを求めることができます。
一般に、ラプラシアンは以下の式で定義される。
$$\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$$
デジタル画像においては、横方向の2次微分と縦方向の2次微分の結果を足し合わせることでラプラシアンの値が得られます。
この一連の処理は、以下のフィルタで表せます。
$$\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}$$
または、別の表現として以下のフィルタも用いられます。
$$\begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{bmatrix}$$
ラプラシアンフィルタでは、方向に依存しないエッジが直接得られます。
しかし、ラプラシアンは本質的に微分を繰り返すため、ノイズを強調しやすいという欠点もあります。
そのため、まずガウシアンフィルタを適用してある程度の平滑化を行ったのち、ラプラシアンフィルタを適用することが一般的である。
この処理は1つにまとめることが可能であり、ラプラシアン・オブ・ガウシアン(Laplacian of Gaussian, LoG)フィルタとして表されます。
LoGフィルタ(Laplacian of Gaussian)
2次元ガウス関数は以下の式で表されます。
$$G(x, y) = \frac{1}{2\pi \sigma^2} \exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right)$$
このガウス関数に対してラプラシアンを適用すると、LoGフィルタが得られます。
$$\nabla^2 G(x, y) = \frac{x^2+y^2-2\sigma^2}{2\pi \sigma^6} \exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right)$$
ガウス分布関数のラプラシアン(LoG)を3Dプロットです。ピークの周囲に正負の値が分布し、エッジ検出に適した特性を持つことが確認できます
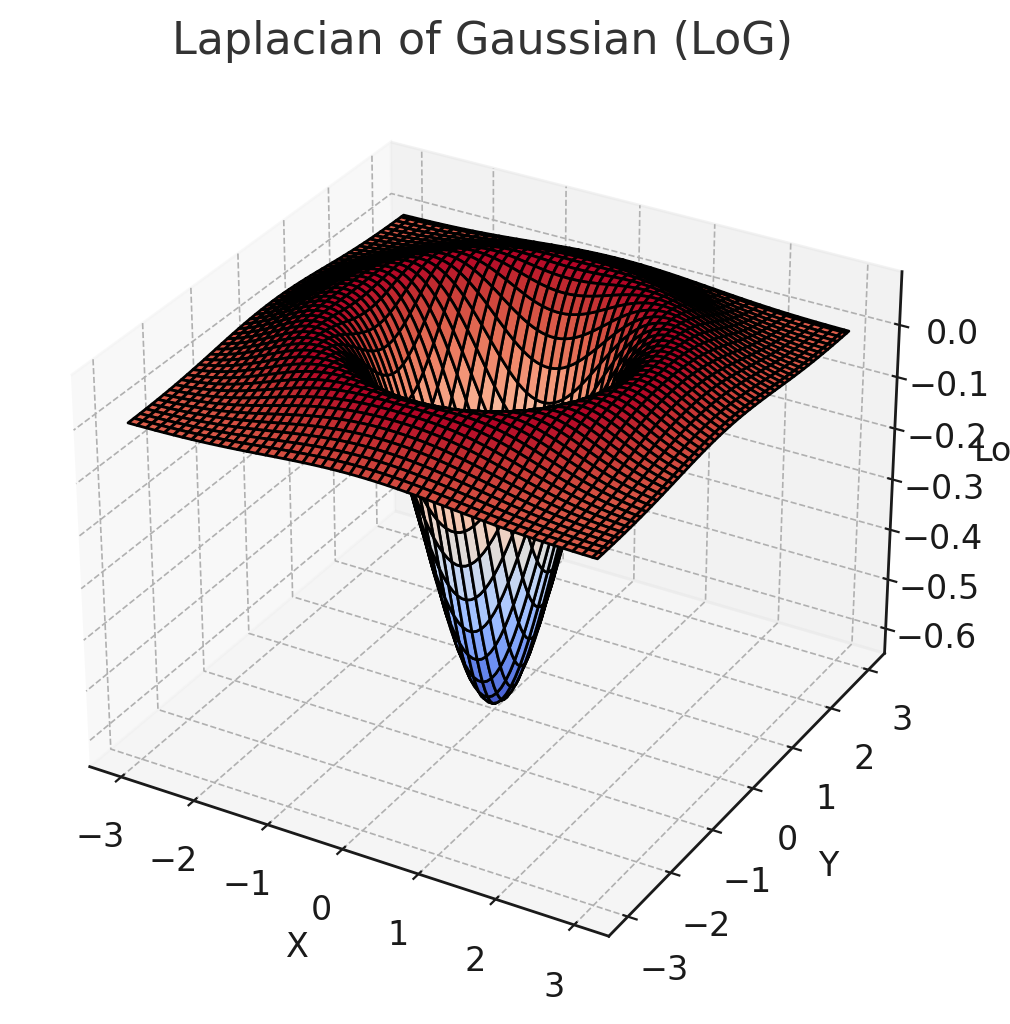
このフィルタを画像に適用することで、平滑化とエッジ検出を同時に行うことが可能になります。

DoGフィルタ(Difference of Gaussian)
また、LoGフィルタは2つの異なる標準偏差を持つガウスフィルタの差分(Difference of Gaussian, DoG)で近似できることが知られています。
標準偏差\(\sigma_1と\)latex \sigma_2を持つ2次元ガウス分布をそれぞG_{\sigma_1}およびG_{\sigma_2}とすると、DoGフィルタは以下のように表される。
$$(x, y) = G_{\sigma_1}
このフィルタを適用することで、ラプラシアンの計算を効率的に近似してエッジを検出することができます。

まとめ
- 2次微分は、横方向および縦方向の差分を2回適用することで求められる。
- ラプラシアンフィルタは、横方向および縦方向の2次微分を足し合わせたもの。
- ラプラシアンフィルタはエッジ検出に有効だが、ノイズを強調するため、ガウシアンフィルタと組み合わせたLoGフィルタがよく用いられる。
- LoGフィルタは、2つの異なるガウシアンフィルタの差であるDoGフィルタによって近似できる。
これらのフィルタを適切に用いることで、エッジ検出の精度を向上させることができます。










ディスカッション
コメント一覧
まだ、コメントがありません