KNNやK-Meansではなぜデータスケーリングが重要なのか
はじめに
KNN(K-Nearest Neighbors)とK-Meansは、最も一般的で広く使用されている機械学習アルゴリズムの一つです。
KNNは教師あり学習アルゴリズムで、分類問題と回帰問題の両方を解決するために使用できます。
一方、K-Meansは教師なし学習アルゴリズムで、データを異なるグループにクラスタリングするために広く使用されます。
これらのアルゴリズムに共通する点は、両方とも距離に基づくアルゴリズムであるということです。
KNNは最も近いk個の隣接点を選択し、その隣接点に基づいて新しい観測値にクラス(分類問題の場合)または値(回帰問題の場合)を割り当てます。
K-Meansは、似ているデータポイントをクラスタリングします。この場合の「似ている」とは、データポイント間の距離で定義されます。データポイント間の距離が小さいほど、データポイントは似ており、逆に距離が大きいほど、似ていないと言えます。
データをスケーリングする理由は?
距離に基づくアルゴリズムは、変数のスケールに影響されます。例えば、データに年齢と収入(月収を表す)という2つの変数があるとします。
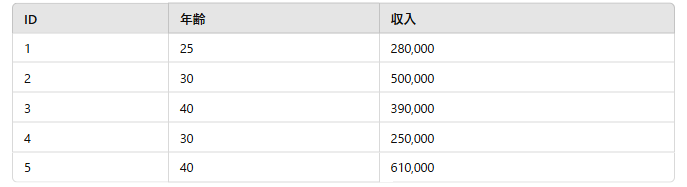
ここで、年齢は25歳から40歳までの範囲で、収入は25万から61万までの範囲です。次に、観測1と観測2の類似度を求めてみましょう。
最も一般的な方法は、ユークリッド距離を計算することです。この距離が小さいほど、ポイントが近く、似ていると見なされます。ユークリッド距離は次のように定義されます。
$$text{Euclidean Distance} = \sqrt{\sum_{i=1}^{n} (x_i – y_i)^2} $$
ここで:
- xix_ixi は1つ目の点の各次元の値
- yiy_iyi は2つ目の点の各次元の値
- nnn は次元数(特徴量の数)
観測1と観測2のユークリッド距離は次のように計算されます:
ユークリッド距離 = [(30–25)^2 + (500000–280000)^2]^(1/2)
この距離は約 220,000.00になります。
ここで注目すべき点は、収入の大きな値が2つのポイント間の距離に影響を与えていることです。これは、距離ベースのモデルの性能に影響を与え、より大きな値(この場合は収入)を持つ変数に高い重みを与えることになります。
このように、アルゴリズムが変数の大きさに影響されないようにする必要があります。アルゴリズムは、大きな値を持つ変数に偏らないようにすべきです。この問題を解決するために、すべての変数を同じスケールに変換することができます。
最も一般的な方法は標準化で、これは変数の平均と標準偏差を計算し、各観測値から平均を引いて、その標準偏差で割る方法です。
$$z = \frac{x – \mu}{\sigma}$$
標準化以外にも、変数を同じスケールに変換する方法があります。例えば、Min-Maxスケーリングです。ここでは、次の式を使用してスケーリングが行われます:
$$ x_{\text{normalized}} = \frac{x – x_{\text{min}}}{x_{\text{max}} – x_{\text{min}}}$$
今回は標準化に焦点を当てます。
では、標準化がどのようにこれらの変数を同じスケールに変換し、距離ベースのアルゴリズムの性能を改善するかを見てみましょう。標準化後のデータは次のようになります:
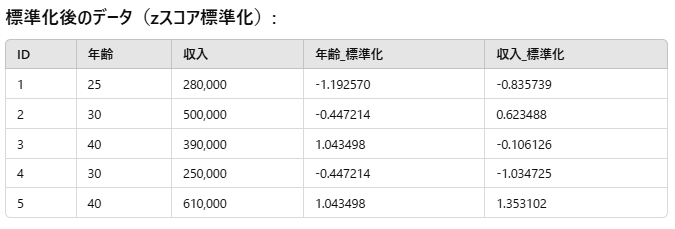
再度、観測1と観測2のユークリッド距離を計算してみましょう:
ユークリッド距離 = [(-0.447+1.193)^2 + (0.6235+0.836)^2]^(1/2)
この時、距離は約1.639になります。この距離は収入変数に偏っていないことがわかります。両方の変数に対して同じ重みが与えられています。
したがって、KNNやK-Meansのような距離ベースのアルゴリズムを適用する際には、すべての特徴量を同じスケールに揃えることが常に推奨されます。








ディスカッション
コメント一覧
まだ、コメントがありません