【画像処理】空間フィルタリングと平滑化
空間フィルタリングの概要
画像処理において、フィルタリング は重要な技術の一つであり、画像のノイズ除去、エッジ強調、平滑化などに用いられます。フィルタリングには大きく分けて 空間フィルタリング と 周波数フィルタリング の2種類があります。
空間フィルタリング(Spatial Filtering) では、画像の各ピクセルとその周囲のピクセルを用いて新しいピクセル値を計算します。これは畳み込み(Convolution)という操作を用いて行われます。
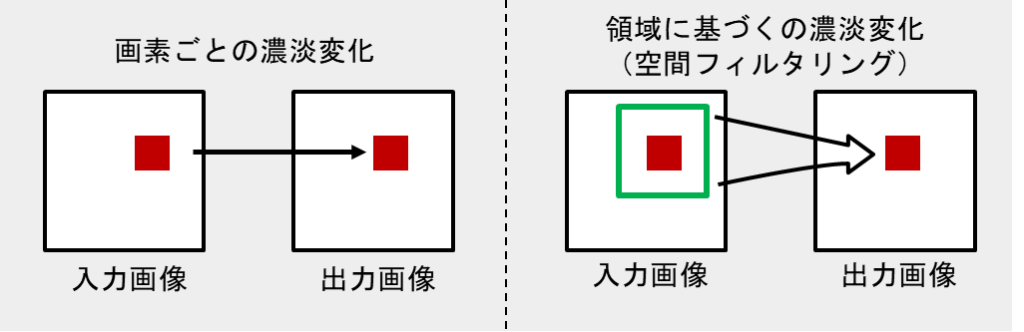
一方で、周波数フィルタリング では、フーリエ変換を用いて画像を周波数成分に変換し、高周波や低周波を選択的に強調・抑制する手法です。本記事では、まず空間フィルタリングについて詳しく解説します。
畳み込みとカーネル
畳み込みは、画像処理における基本的な演算であり、画像と カーネル(Kernel) と呼ばれる小さな行列を用いて新しい画像を生成する操作です。カーネルの値を適切に設定することで、平滑化やエッジ検出などの効果を得ることができます。
畳み込みは以下のような数式で表されます: $$I'(x, y) = \sum_{i=-k}^{k} \sum_{j=-k}^{k} K(i, j) \cdot I(x+i, y+j)$$
ここで:
- I(x, y) は元の画像のピクセル値
- I'(x, y) はフィルタ適用後のピクセル値
- K(i, j) はカーネルの値
- k はカーネルのサイズ(例:3×3ならk=1)
畳み込みの計算手順:
- カーネルを画像の特定のピクセル位置に重ねる。
- 重なった領域のピクセル値とカーネルの値を要素ごとに掛け算する。
- その結果をすべて足し合わせる。
- 計算結果を新しい画像の対応するピクセルに設定する。
- 画像全体に対してこの操作を繰り返す。
下の例だと、3*3のカーネルを入力画像中央の赤いピクセル(80)に適用します。
カーネルと対象範囲(3*3)の積和を計算すると250となります。
(-1)*30+(-1)*30+(-1)*30+(-1)*30+9*80+(-1)*80+(-1)*90+(-1)*90+(-1)*90 = 250

カーネル(フィルタ)の例
カーネルはフィルタの種類によって異なります。代表的なカーネルをいくつか紹介します。
平均フィルタ(Mean Filter)
フィルタによって覆われる領域内の画素値の平均値を求めます。
フィルタのサイズが大きくなると平均化の効果がより大きくなります。
$$K = \frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix}$$

ガウシアンフィルタ(Gaussian Filter)
ガウス分布の特性を利用したフィルタです。注目画素からの距離に応じて2次元ガウス分布による重みをつけます。
単純な平均化フィルタに比べて見た目に大きな違いはないものの、より滑らかで自然な平滑化の効果が期待できます。
$$K(x, y) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2 + y^2}{2\sigma^2}}$$

バイラテラルフィルタ(Bilateral Filter)
バイラテラルフィルタは、空間的な近さと色の類似度の両方を考慮した平滑化を行います。
注目画素からの距離による重みに加えて、注目画素との画素値の差に応じて同様にガウス分布に従う重みをつけた平均化を行うフィルタです。
数式は以下のようになります: $$I'(x, y) = \frac{1}{W_p} \sum_{i, j} I(i, j) \cdot f_s(||(x, y) – (i, j)||) \cdot f_r(|I(x, y) – I(i, j)|)$$
ここで:
- \(fs(d)=e^{-\frac{d^2}{2\sigma_s^2}} \)は空間的な距離に基づく重み
- \(fr(r)=e^{-\frac{r^2}{2\sigma_r^2}} \)は画素値の類似度に基づく重み
- \(W_p\) は正規化係数
このフィルタはエッジを保持しながらノイズを除去するのに適しています。

ノンローカルミンフィルタ (Non-Local Means Filter)
ノンローカルミーンフィルタ (Non-Local Means Filter) は、バイラテラルフィルタの発展形であり、類似パターンの画像領域を考慮して重み付けを行う手法です。
周辺画素だけでなく、画像全体の中で類似したパターンを持つ領域の画素を考慮し、重み付けを行う。そのため、エッジを保持しつつノイズを低減する効果が高くなります。
ノンローカルミーンフィルタでは、重み w(i,j,m,n) は以下の式で計算されます。
$$w(i, j, m, n) = \exp \left( -\frac{\sum \sum ( f(i+s, j+t) – f(i+m+s, j+n+t) )^2 }{ 2\sigma^2 } \right)$$
- ここで、重みは注目画素と周辺画素の類似性に基づいて決定される。
- σはノイズ分散に関連し、フィルタの強さを調整するパラメータ。
- 類似度は、小領域ごとの画素値の違いを二乗して計算される。

メディアンフィルタ(Median Filter)
メディアンフィルタは領域内の中央値を出力するフィルタです。
$$I'(x, y) = \text{median}(I(x+i, y+j)), \quad \forall i, j \in \text{kernel}$$
インパルスノイズ(塩胡椒ノイズ)に強いフィルタです。

まとめ
| フィルタ名 | 特徴 | 計算コスト |
|---|---|---|
| 平均フィルタ | 簡単に実装できるが、エッジがぼやける | 低 |
| ガウシアンフィルタ | エッジを残しやすい | 低 |
| バイラテラルフィルタ | エッジを保持しながら平滑化 | 高 |
| ノンローカルミーン | 非局所的な情報を利用し高品質なノイズ除去 | 非常に高 |
| メディアンフィルタ | インパルスノイズに強い | 中 |








ディスカッション
コメント一覧
まだ、コメントがありません