【Python_点群処理】回転行列を使った3次元点群の回転
回転
3次元点群を回転行列を使用して回転させてみます。
回転行列は3×3行列で表現され、x軸、y軸、z軸周りの回転は以下のようにあらわすことができます。
x軸まわりの回転
$$rot_x = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta_x & -\sin\theta_x \\ 0 & \sin\theta_x & \cos\theta_x \end{bmatrix}$$
y軸まわりの回転
$$rot_y = \begin{bmatrix} \cos\theta_y & 0 & \sin\theta_y \\ 0 & 1 & 0 \\ -\sin\theta_y & 0 & \cos\theta_y \end{bmatrix}$$
z軸まわりの回転
$$rot_z = \begin{bmatrix} \cos\theta_z & -\sin\theta_z & 0 \\ \sin\theta_z & \cos\theta_z & 0 \\ 0 & 0 & 1 \end{bmatrix}$$
Pythonでの実装
Rotation_xyz を定義してPythonで3次元点群の回転をしてみます。
入力は(numpoints,3)の点群データと、x,y,z周りの回転角(deg)です。
戻り値は、回転後の点群と回転行列になります。
def Rotation_xyz(pointcloud, theta_x, theta_y, theta_z):
theta_x = math.radians(theta_x)
theta_y = math.radians(theta_y)
theta_z = math.radians(theta_z)
rot_x = np.array([[ 1, 0, 0],
[ 0, math.cos(theta_x), -math.sin(theta_x)],
[ 0, math.sin(theta_x), math.cos(theta_x)]])
rot_y = np.array([[ math.cos(theta_y), 0, math.sin(theta_y)],
[ 0, 1, 0],
[-math.sin(theta_y), 0, math.cos(theta_y)]])
rot_z = np.array([[ math.cos(theta_z), -math.sin(theta_z), 0],
[ math.sin(theta_z), math.cos(theta_z), 0],
[ 0, 0, 1]])
rot_matrix = rot_z.dot(rot_y.dot(rot_x))
rot_pointcloud = rot_matrix.dot(pointcloud.T).T
return rot_pointcloud, rot_matrix
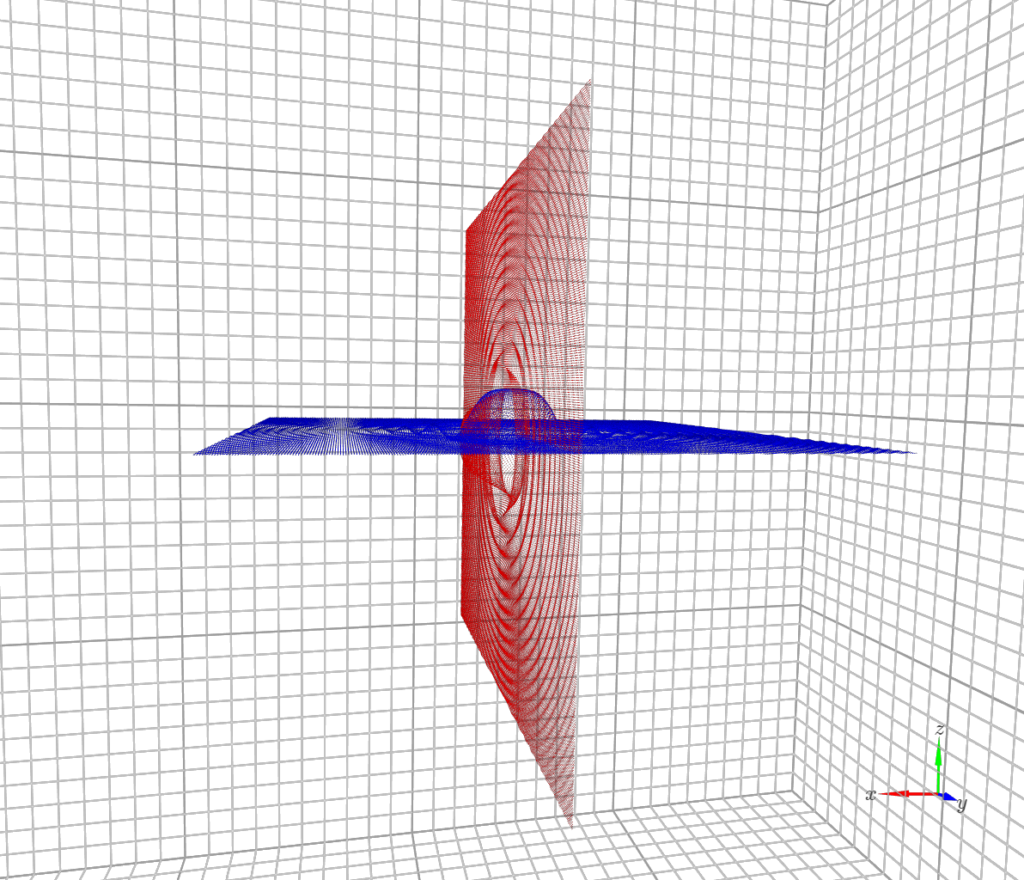
y軸周りに90度回転させてみます。
theta_x = 0
theta_y = 90
theta_z = 0
rot_pointcloud, rot_matrix = Rotation_xyz(test_data, theta_x, theta_y, theta_z)青い点群が回転前のデータ、赤い点群が回転後です。
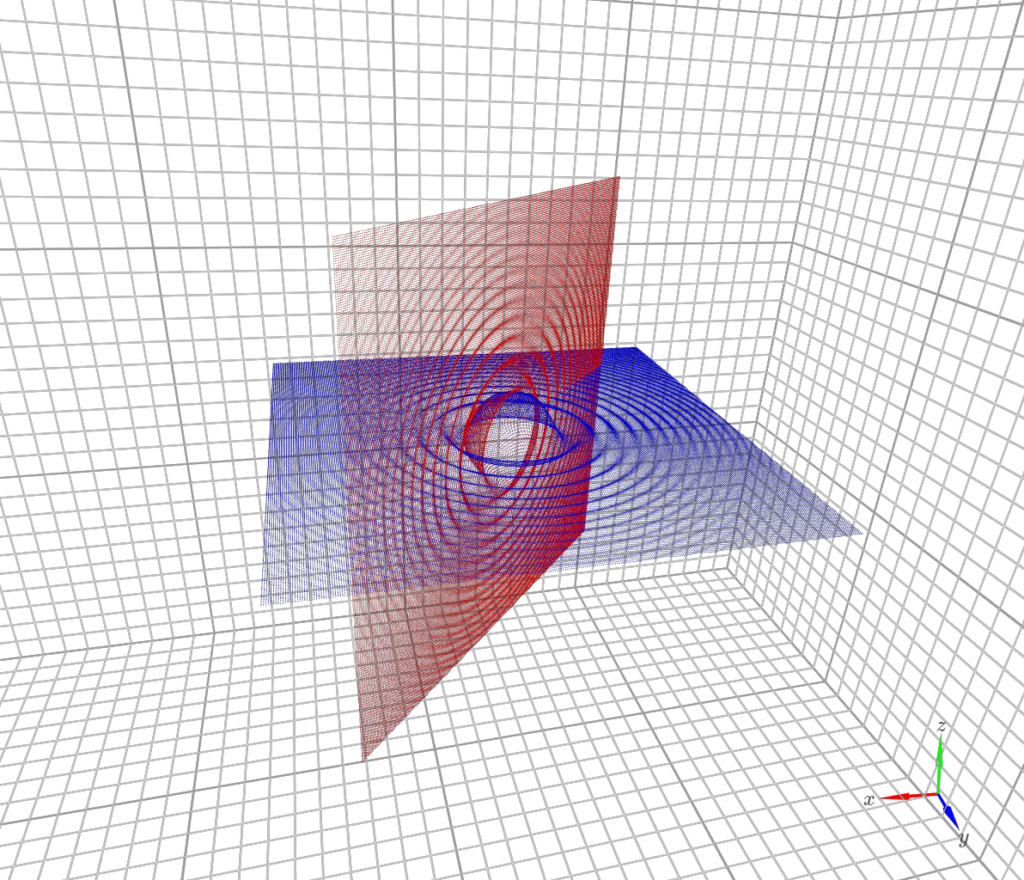
次にx軸周りに45度、y軸周りに90度回転させてみます。
theta_x = 45
theta_y = 90
theta_z = 0
rot_pointcloud, rot_matrix = Rotation_xyz(test_data, theta_x, theta_y, theta_z)青い点群が回転前のデータ、赤い点群が回転後です。
青い点群をy軸周りに90度回転させたのち、x軸周りに45度回転させると赤い点群になります。







ディスカッション
コメント一覧
このコメントは管理者のみ閲覧できます。
ご質問ありがとうございます。
私のコードにミスがあり、おそらく関数内で定義されているpointcloud という変数名がopen3dのpointcloudオブジェクトと認識されてしまっているかと思います。
def Rotation_xyz 内の、pointcloudという変数名を適当な変数名(pclなど)にして試してみていただけますでしょうか。
早速のご返信、ありがとうございました。
def Rotation_xyz内のpointcloudをpdに変更してみましたが、同じエラー(AttributeError: ‘open3d.cpu.pybind.geometry.PointCloud’ object has no attribute ‘T’)が出ました。
私の方でpointcloud、pdとしたデータは、o3d.geometry.PointCloud.create_from_rgbd_imageで作成したデータなので、行列になっていない(?)ため、転置行列が作れないということでこのエラーになっているのではないかと予想しています。
bearjiro様のtest_dataはどのように作られたものなのでしょうか?
例えば、xyz形式で行列になっているデータだったなら、エラーは出ないのかもしれません。
以上、よろしくお願いします。
test_dataは、おっしゃる通りxyz形式の行列ですのでo3dの点群データを同じ形式に変換していただく必要があります。
このあたりを参考にしていただければと思います。
https://tech-deliberate-jiro.com/np-to-o3d/
何度もありがとうございました。
np.asarrayでNumpyの形式に変換できるのですね。
これで解決しそうです。