※当サイトはPRを含みます

【3D点群処理】点群データにおける法線とOpen3Dを用いた法線の推定

2023年7月31日

点群における法線とは

点群データにおける法線は、各点が存在する3次元空間における「面」の向きを示します。

具体的には、ある点を中心とした近傍の点群が形成する面に対して垂直な方向を指します。

この法線はベクトルとして表現され、その方向と長さ（大きさ）によって面の向きと傾斜を表現します。

点群データにおける法線の計算は、3次元形状の再構成、表面の滑らかさの推定、物体の向きの推定、3Dレンダリングなど、様々なアプリケーションで重要な役割を果たします。

例えば、3DスキャンやLIDAR（光検出と距離測定）などで得られた点群データから物体の3次元形状を再構成する際には、各点の法線を計算することで物体の表面の形状や向きを推定することができます。

また、3Dレンダリングでは、法線を用いて光の反射や陰影の計算を行い、リアルな画像を生成します。

法線を用いた陰影の作成方法

また、点群データが表現する物体の表面が滑らかである場合（例えば、球や平面など）、近傍の点の法線はほぼ同じ方向を指します。

一方、表面が粗いまたはエッジがある場合（例えば、角や突起など）、法線の方向は大きく変わる可能性があります。このように、法線の分布を分析することで、物体の表面の特性を理解することも可能です。

法線を使用したエッジ抽出の例

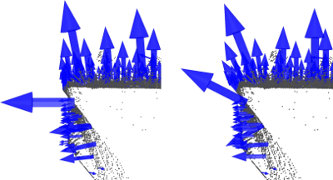
PCAを使った法線の計算

法線の計算は以下の手順で行います。

①近傍点の選定

法線を計算したい点を選び、その点の近傍点を選択します。

近傍点の選択方法はいくつかありますが、一般的にはk-最近傍法（k-nearest neighbors）や半径内の点を選択する方法（radius-based neighbor selection）が用いられます。

②重心の計算

選択した近傍点の重心（平均座標）を計算します。重心は各座標値の平均で求めることができます。

③共分散行列の計算

選択した近傍点の共分散行列を計算します。

共分散行列は、各座標軸における点の分布の広がり（分散）と、異なる座標軸間の点の分布の関連性（共分散）を表します。

共分散行列の計算方法は以下のようになります。

データ行列を \( X \) とし、\( X \) は \( m \times n \) の行列で、\( m \) はデータ点の数、\( n \) は次元数とします。 平均ベクトルを \( \mu \) とし、\( \mu \) は \( n \) 次元ベクトルで、各成分 \( \mu_i \) は \( X \) の \( i \) 列目の平均値とします。つまり、\( \mu_i = \frac{1}{m} \sum_{j=1}^{m} X_{ji} \) となります。 次に、データ行列 \( X \) から平均ベクトル \( \mu \) を引いた行列を \( Y \) とします。これにより、データは平均0となります。 そして、共分散行列 \( C \) は以下のように計算されます。 \[ C = \frac{1}{m-1} Y^T Y \] ここで、\( Y^T \) は行列 \( Y \) の転置を表します。この計算により、共分散行列 \( C \) は \( n \times n \) の行列となり、\( C \) の \( (i, j) \) 成分はデータの \( i \) 次元と \( j \) 次元の共分散を表します。

以上が共分散行列の計算方法です。この共分散行列は、データの各次元間の関係性を表す重要な情報を持っています。

④固有値と固有ベクトルの計算

共分散行列の固有値と固有ベクトルを計算します。

固有値は共分散行列の各方向の分散を表し、固有ベクトルはそれらの方向を表します。

共分散行列の固有値と固有ベクトルを求める方法は以下のようになります。 共分散行列を \( C \) とします。 共分散行列 \( C \) の固有値 \( \lambda \) と固有ベクトル \( v \) は、以下の等式を満たします。 \[ Cv = \lambda v \] つまり、各固有ベクトル \( v \) は、\( C \) によって乗算された結果が \( v \) のスカラー倍となるようなベクトルです。そのスカラーが、\( v \) に対応する固有値 \( \lambda \) です。 固有値は、対応する固有ベクトルによって定義される方向に沿ったデータの分散を表します。

⑤法線の決定

最小の固有値に対応する固有ベクトルが、点群が形成する表面に対する法線となります。

これは、点群が形成する表面は、分散が最大となる2つの軸によって張られる平面に最も近いと考えられるからです。

Open3Dで法線推定

Open3Dでは法線を推定するプログラムが用意されています。

import open3d as o3d
# numpyの点群データをopen3d に変換。 test_data -> numpy array (n,3)
pcd=o3d.geometry.PointCloud()
pcd.points = o3d. utility.Vector3dVector(test_data)
# 法線ベクトルの推定（KDTreeによる近傍点探索を使用）
pcd.estimate_normals(
    search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
# Open3dで可視化
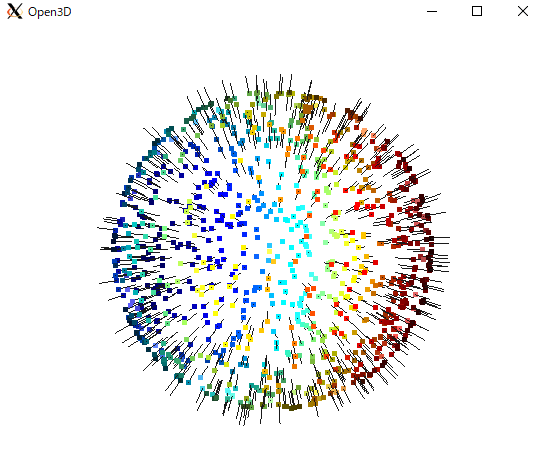
o3d.visualization.draw_geometries([pcd], point_show_normal=True)

各点に対して出ている黒い線が法線ベクトルです。

面に対して垂直になるように表示されています。

おすすめ参考書

点群処理OPEN3D,point cloud,python,点群処理