【Python_3D点群処理】点群のダウンサンプリング：FPSについての解説と実装

2022年5月24日

1. はじめに
2. FPSの解説
3. FPSのPythonでの実装
4. まとめ
5. おすすめ参考書

はじめに

3D点群処理で扱うデータはとても大きいため、そのまま扱うと処理に時間がかかってしまいます。
そのため事前に元の点群データから一定のポイント数だけを抽出するダウンサンプリングを実施するのが一般的です。

ここで重要なのが
データの数は減らしても、情報量は減らしたくない
ということです。

どういうことかというと、ある点群の中から同じサンプル数だけをサンプリングして処理したいときに
以下のように偏った箇所からとってしまうと元の点群が何かわからなくなってしまうため意味がありません。

つまり、元の点群の情報をできるだけ維持したまま上手にサンプリングすることが必要になります。

FPSの解説

今回はダウンサンプリングの手法で一般的なFPSについて解説します。
FPSとはFarthest Point Sampling の略です。
簡単に言うと、”遠くの点から順番に取っていく”　手法になります。

A,B,C,Dの4点を例に、FPSでサンプリングしていきます。

キーワードは 「各点から最近傍点までの距離(distance)」 と 「サンプリングした点から各点までの距離(dist)」
になります。

それでは順を追ってみていきます。
⓪ 初期値として「各点から最近傍点までの距離（distance）」を仮置きします。（今回は10とします）

1回目のサンプリング(点A)
① ランダムに最初の点Aをサンプリングします。(サンプリング済みの点は黒色で表示しています)

② サンプリングした点Aから各点までの距離(dist)を求めます。
図から点A-点B間の距離は4、点A-点C間の距離は6、点A-点D間の距離は1です。
このとき、点A-点A間の距離は0となります。

③ 点Aから各点までの距離（dist）と各点から最近傍点までの距離（distance）を比較します。

dist < distance となっている点があれば、今回サンプリングした点Aがその点の最近傍点になります。
1回目のサンプリングなのでdist と distance　を比較するとすべての点の最近傍点までの距離(distance)が更新され、distanceは[0 4 6 1]になります。

④ 更新されたdistanceの中で最も大きい数値の点を次のサンプリング点とします。
したがって2回目のサンプリングは点Cになります。

※以降は②~④の処理を指定のサンプリング数になるまで繰り返します。

2回目のサンプリング(点C)
⑥ 点Cから各点までの距離：distを求めます。
図から点C-点A間の距離は6、点C-点B間の距離は3、点C-点D間の距離は5です。
このとき、点C-点C間の距離は0となります。

⑦ 点Cから各点までの距離（dist）と各点から最近傍点までの距離（distance）を比較します。

点Bがdist < distanceとなっているので今回サンプリングした点Cが点Bの最近傍点になります。
また今回サンプリングした点Cのdisatanceも0となり、distanceは[0 3 0 1]となります。

⑧ 更新されたdistanceの中で最も大きい数値の点を次のサンプリング点とします。
したがって3回目のサンプリングは点Bになります。

3回目のサンプリング(点B)
⑨ 点Bから各点までの距離：distを求めます。
図から点B-点A間の距離は4、点B-点C間の距離は3、点B-点D間の距離は5です。
このとき、点B-点B間の距離は0となります。

⑩ 点Bから各点までの距離（dist）と各点から最近傍点までの距離（distance）を比較します。

今回サンプリングした点Cのdisatanceが0となり、distanceは[0 0 0 1]となります。

⑪ 更新されたdistanceの中で最も大きい数値の点を次のサンプリング点とします。
したがって最後4回目のサンプリングは残った点Dになります。

このように遠くの点を順番に取るようにサンプリングすることで点群の形状をうまく残したままダウンサンプリングすることができます。
しかし、ランダムダウンサンプリングなどと比較すると処理に時間がかかってしまうのがデメリットとしてあげられます。

FPSのPythonでの実装

FPSをPythonで書くと以下のようになります。
pointが入力点群、npointがサンプル数です。

def farthest_point_sample(point, npoint):
    """
    Input:
        xyz: pointcloud data, [N, D]
        npoint: number of samples
    Return:
        centroids: sampled pointcloud index, [npoint, D]
    """
    N, D = point.shape
    xyz = point[:,:3]
    centroids = np.zeros((npoint,))
    distance = np.ones((N,)) * 1e10
    farthest = np.random.randint(0, N)
    for i in range(npoint):
        centroids[i] = farthest
        centroid = xyz[farthest, :]
        dist = np.sum((xyz - centroid) ** 2, -1)
        mask = dist < distance
        distance[mask] = dist[mask]
        farthest = np.argmax(distance, -1)
    point = point[centroids.astype(np.int32)]
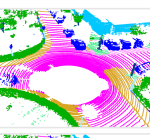
    return point

以下が実行結果です。

FPSはランダムサンプリングに比べて輪郭がはっきりとしていて、よりオリジナルの情報を保ったままサンプリングできていることが分かります。ただ、計算量が多いため点数が多いと処理に時間がかかってしまいます。