【Python_3D点群処理】点群における凸包の計算,内外判定(convex-hull)
はじめに
今回はPythonを使って点群の内部/外部の判定や範囲を指定した点群の抽出などをしたいと思います。
イメージとしてはこんな感じのことができます。
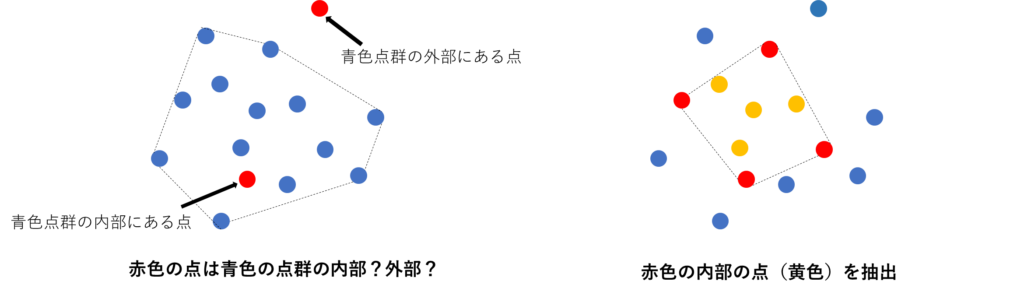
凸包(convex hull)というアルゴリズムを使用して実際に点群の抽出をしてみます。
凸包(convex hull)とは(理論)
凸包(convex hull)とは与えられた点をすべて含んでいる最小の凸多角形のことです。
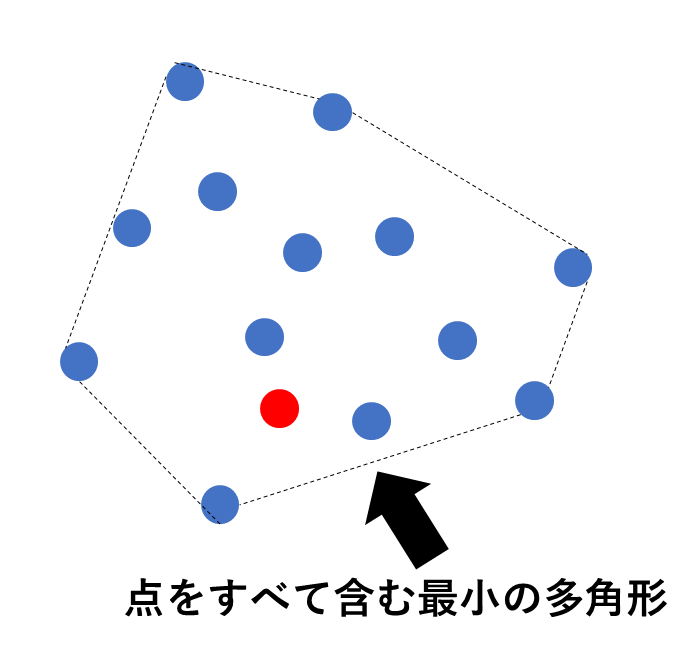
凸包を計算するアルゴリズムをいくつか紹介します。
ギフト包装法(Gift wrapping)
① xが最小かつyが最小の点を最初の注目点とする。
② 注目点とその他の点との偏角を求めて最も大きい点を次の注目点にする

③ ②が①の点になるまで繰り返す
グラハムスキャン(Graham scan)
① 点群の重心点を求める
② 重心点に対して各点に対して偏角を求める
③ 角度が小さい順にソートして、xが最小かつyが最小の点を凸包の始点とする
④ ソートした順に、点をたどり、次の点が前回の点より時計回りの方向にある場合は前回の点を凸包の頂点から削除
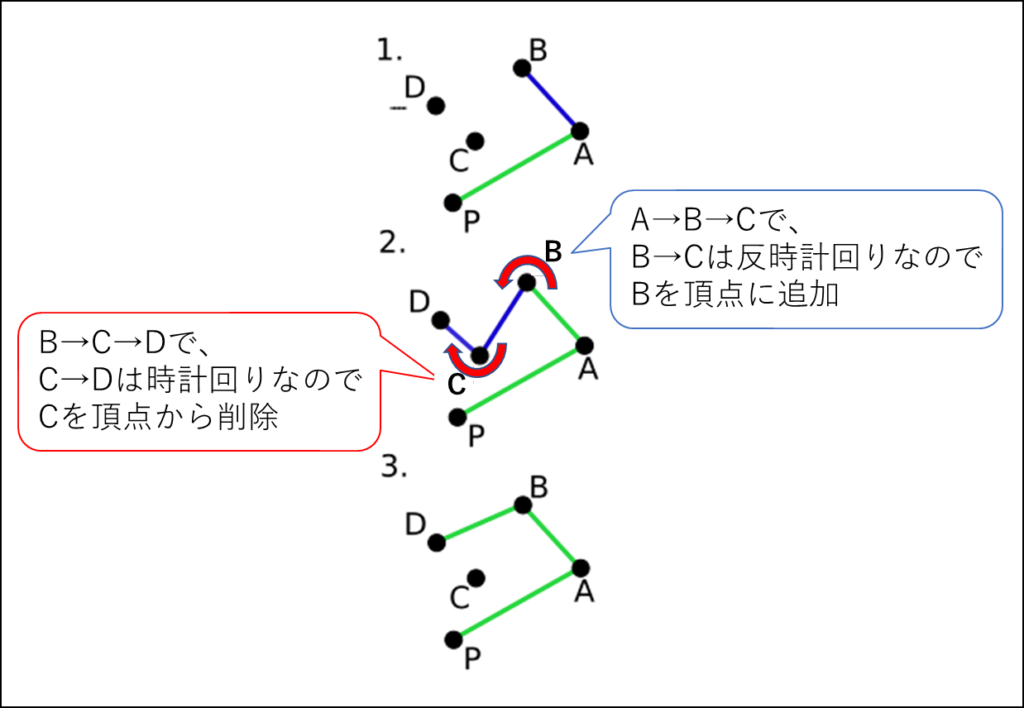
⑤ 初めの点に戻るまで③‐④を繰り返す
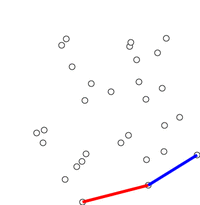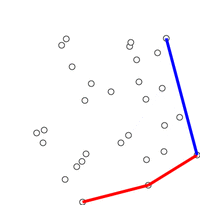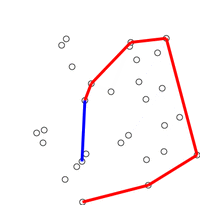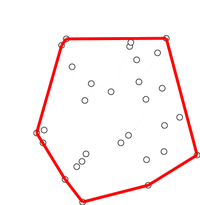
クイックハル(Quick hull)
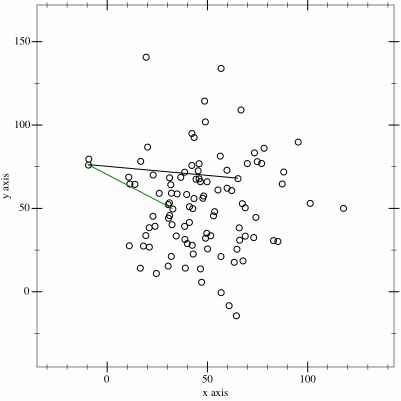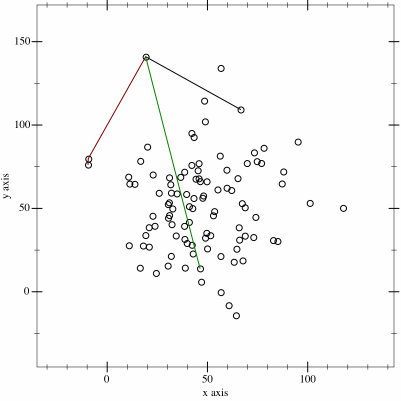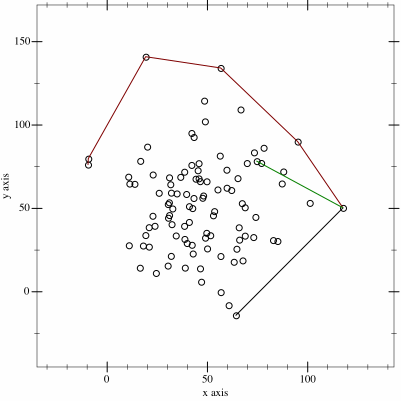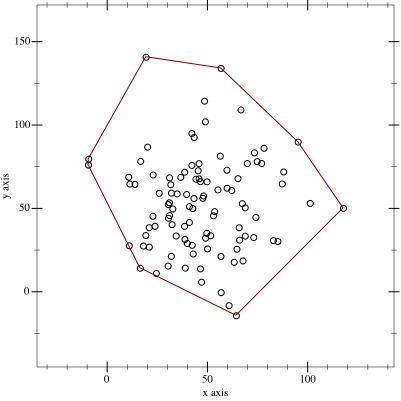
① xが最小の点と最大の点を求めて2点間の線を引く
② 引かれた直線で点群を2つに分割する
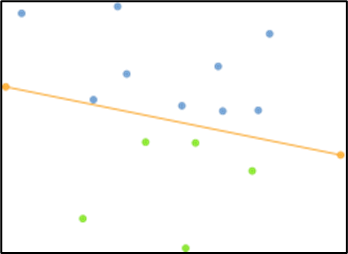
③ 直線から最も遠い点を求めて三角形を作る
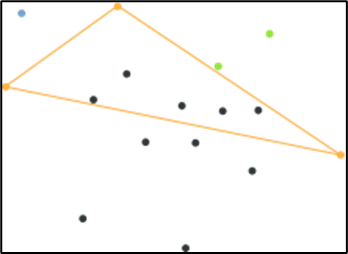
④ 三角形の内側にある点は無視をする
⑤ 点がなくなるまで②‐④を繰り返す
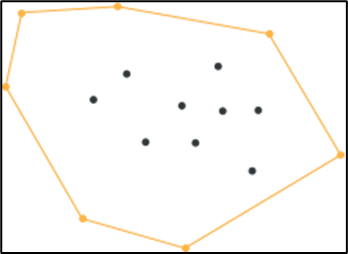
PythonでQuick hullを実装
クイックハルは凸包計算アルゴリズムの中でも高速で三次元にも対応できるという特徴があるのでPythonで実装してみます。
凸包の計算
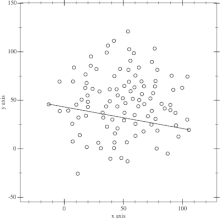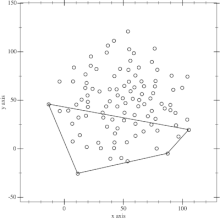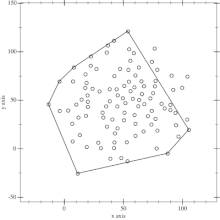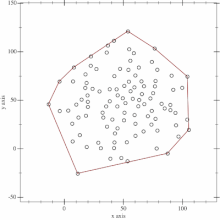
はじめに下のような点群対して凸包を計算してみます。
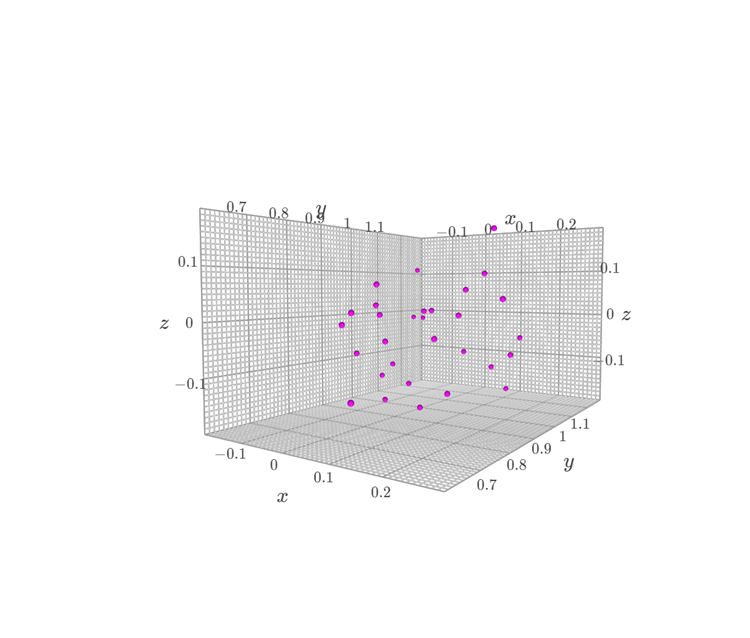
コードは以下の通りです。
scipyで凸包が計算できます。凸包の頂点を青色でプロットし、稜線を引きます。
import k3d
from scipy.spatial import ConvexHull
# 点群をプロット
plot = k3d.plot()
plot +=k3d.points(points, point_size=0.02, color = 0xff00ff)
plot.display()
# 凸包を計算
hull = ConvexHull(points)
# 凸包を描画
for simplex in hull.simplices:
# 凸包の頂点を描画
plot +=k3d.points(points[simplex], point_size=0.02, color = 0x0000ff)
# 凸包の稜線を描画
plot +=k3d.line(points[simplex], point_size=0.02, color = 0x0000ff)
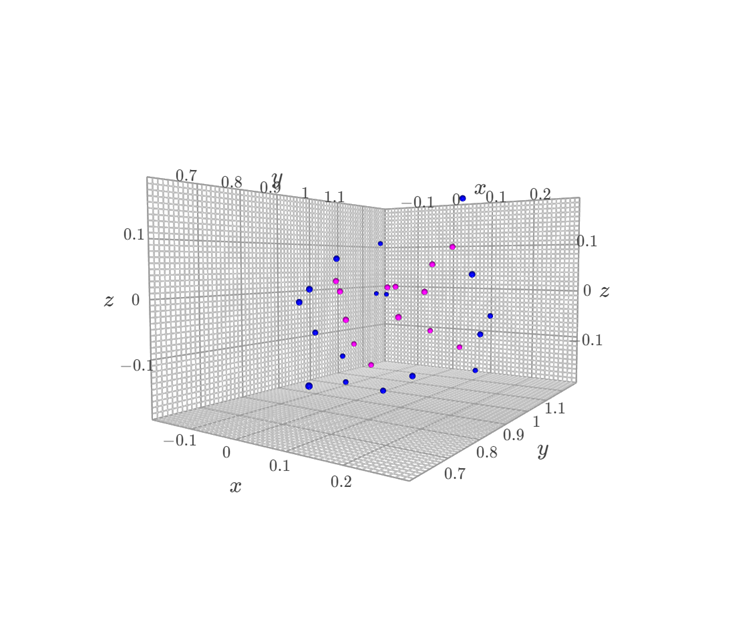
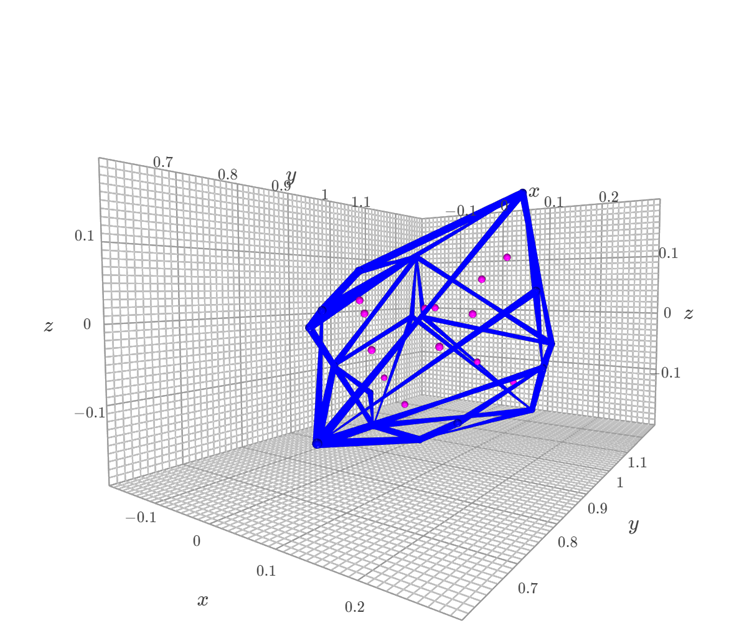
実行結果です。上が頂点のみのプロット、下が稜線を加えた結果になります。
内部の点をすべて含んだ凸包が作成できました。
点の内外判定
次に関数in_hullを定義して、点の内外判定をしてみます。
ピンクの点群内に、赤色の2点が存在しているか判定します。
内部にある場合は点を青→赤色に変更します。
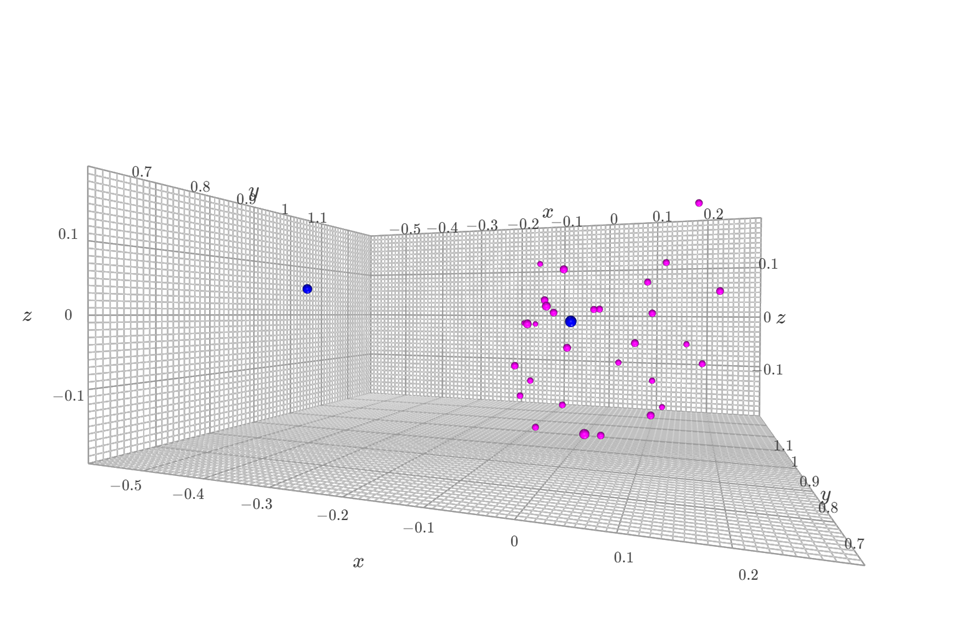
コードは以下の通りです。
in_hullでは、pがhullの内部にあるか計算します。
pはk次元、NポイントのN×k、hullは、k次元のMポイント座標でM×kサイズです。
import k3d
from scipy.spatial import Delaunay
# 凸包で点の内外判定をする
def in_hull(p, hull):
if not isinstance(hull,Delaunay):
hull = Delaunay(hull)
return hull.find_simplex(p)>=0
# 点群をプロット
# points:元の点群
# test:内外判定する点群
plot = k3d.plot()
plot +=k3d.points(points, point_size=0.02, color = 0xff00ff)
plot +=k3d.points(test, point_size=0.03, color = 0x0000ff)
plot.display()
# testがpoint内にあるかどうかを判定する
hull = in_hull(test,points)
# testがpointの内部にある場合、点の色を赤に変更
for h,p in zip(hull,test):
if h == True:
plot +=k3d.points(p, point_size=0.03, color = 0xff0000)
else:
plot +=k3d.points(p, point_size=0.03, color = 0x0000ff)実行結果です。ピンクの点群の内部の点は赤色、外部の点は青になっています。
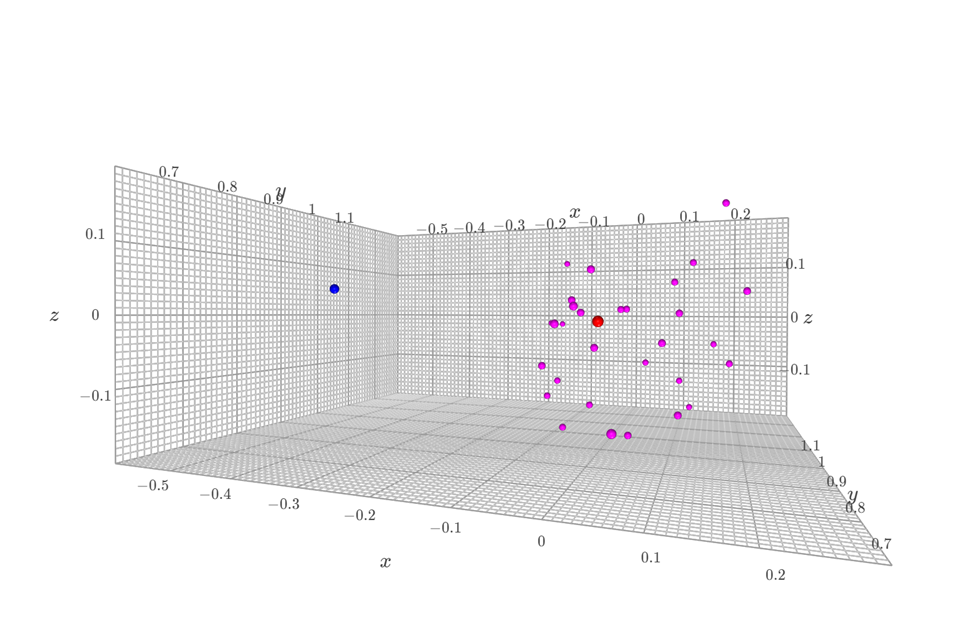








ディスカッション
コメント一覧
まだ、コメントがありません